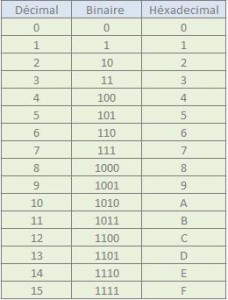
Les mathématiques informatiques peuvent changer la vision des calculs que l’on apprend à l’école, on apprend ainsi que 10 devient A et que 1000 équivaut à 8.
On l’utilise cela en informatique pour passer d’un language binaire composé de 1 et de 0
( ex : 011010011101 ) avec ce que l’on appel une base de 2.On peut utiliser également après le binaire le décimal ce que l’on connait tous et que l’on pratique tout les jours lorsque l’on fait nos courses dans un hypermarché. Il est composé de chiffre 1 2 3 4 5 6 7 8 9 0 ( Ex : 2600 ) avec une base de 10.
Il reste maintenant l’Hexadécimal qui consiste via un système de correspondance à crypter des données.
Ils peuvent ainsi être utilisé sur un réseau, pour crypter votre clée Wifi ( Souvenez vous, on vous demande généralement 8 ou 16 caractères).
C’est ici que l’Hexadécimal avec ca base de 16 ( ex: 6B4F )
On à donc ici trois formes bien distinctes qui pourtant donne toute la même résultat suivant comment on veut l’exprimer.
A quoi correspond les bases 2, 10, 16 ?
Hexadécimal : 16 – Décimal : 10 – Binaire : 2Je vais prendre un exemple cela sera plus facilement explicable.
J’utiliserai ici le nombre décimal : 8A2F
En utilisant mon exemple : 8A2F. Je compte l’unité, je suis dans les millier donc 3 zéros. Si j’avais été en centaine je n’aurai que deux zéros ( 8A2 par exemple).
Je précise cela car c’est important pour la suite du calcul.
Voici le calcul final, j’explique au dessous.
8*16(3)+10*(16)2+2*16(1)+15*16(0)
Littéralement on peut le lire : 8 fois 16 à la puissance 3 plus 10 fois 16 à la puissance deux plus deux fois 16 à la puissance un plus quinze fois seize à la puissance zéro.
Pour effectuer cette opération il faut connaître le tableau de conversion ci dessus. AInsi A devient 10 et F devient 15.
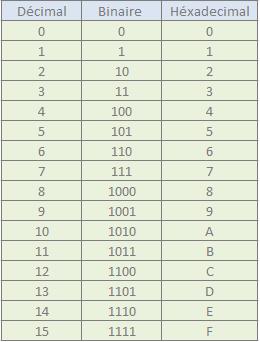
On applique ainsi suivant l’unité ( millier, centaine ) un nombre décroissant de la puissance. Le résultat finale vous donnera la valeurs décimal de votre valeurs hexadécimal, ici : 35375.
Ce type d’information est de calcul sont présente dans nombres de domaine comme dans l’économie ou des techniques sont basé sur ce type de calcul.
Vous pouvez consulter ces explications sur la méthode binaire